Filtres du premier ordre⚓
Attention : Compte-rendu
Un compte-rendu est attendu :
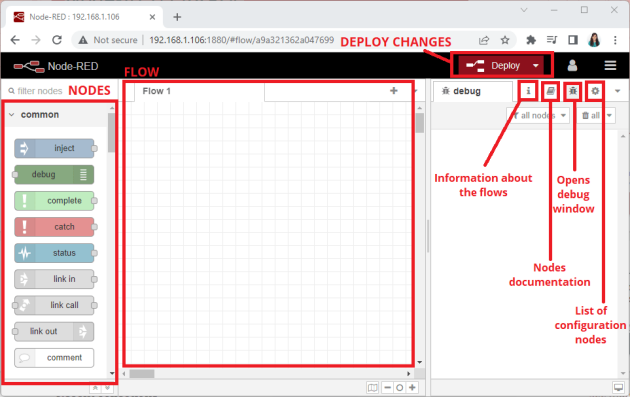
Copie d'écran du câblage sous TinkerCAD
Le tableau (CALC) des différentes mesures effectuées
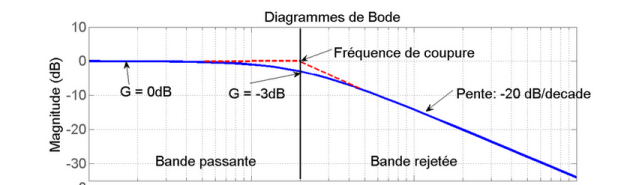
Le diagramme de Bode du filtre
La même chose pour le passe-haut
Différents types de filtres et symboles
Passe bas
Le Filtre passe-bas & pour fonction d'atténuer les fréquences supérieures à sa fréquence de coupure\( f_c\) et ce, dans le but de conserver uniquement les basses fréquences. La fréquence de coupure du filtre est la fréquence séparant les deux modes de fonctionnement idéaux du filtre : passant ou bloquant.
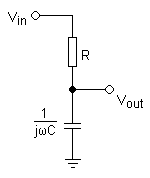
La manière la plus simple de réaliser physiquement ce filtre est d'utiliser un circuit RC constitué d'une résistance R et d'un condensateur de capacité C. Ces deux éléments sont placés en série avec la source \(V_{in}\) du signal. Le signal de sortie \(V_{out}\) est récupéré aux bornes du condensateur. L'amplification s'écrit :
\(A(f) = \frac{V_{out}}{V_{in}} = \frac{1}{1+j 2 \pi RC f}\)
Le gain en décibel s'écrit ainsi :
\(G_{dB}(f) = 20 \log (|A(f)|)\)
On peut montrer que pour une certaine fréquence appelée fréquence de coupure
\(f_c = \frac{1}{2 \pi RC}\)
Le gain vaut -3dB
Lorsque \(f<<f_c\) l'amplification \(A(f)\) proche de1 et G proche de 0.
Lorsque \(f>>f_c\) l'amplification \(A(f)\) proche de 0 et G proche de \(-\infty\).
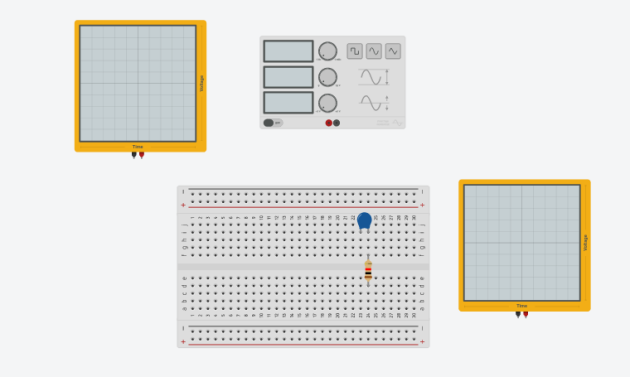
Pour tracer le Gain de ce filtre en fonction de la fréquence, on a besoin d'un GBF (générateur de signaux basses fréquences) et d'un oscilloscope. La tension d'entrée est sinusoïdale centrée sur 0. Les amplitudes des signaux d'entrée et de sortie sont mesurée pour différentes valeur de fréquence (10Hz - 200kHz).
Finir le câblage ci-dessous pour réaliser le filtre passe bas :
Réaliser le circuit en réel (R = 1kΩ) et C = 100 nF en branchant le GBF et l'oscilloscope.
Configurer l'oscilloscope (touche Measure) pour mesurer la fréquence, l'amplitude max de l'entrée \(V_{in}\) et de la sortie \(V_{out}\)
Reporter dans un tableur les valeurs de la fréquence, de l'amplitude max de \(V_{in}\) et de \(V_{out}\)
On s'intéresse ici à la variation gain G en dB en fonction de la fréquence. Dans le tableur ajouter une dernière colonne qui calcule :
\(20 \log (\hat{V}_{out}/\hat{V}_{in})\)
Tracer le diagramme du gain en fonction de la fréquence.
Configurer l'axe des x en échelle logarithmique.
Identifier graphiquement la fréquence de coupure à -3dB
Calculer sa valeur théorique.
Passe haut
Ce filtre très proche du précédent constitué d'une résistance R et d'un condensateur de capacité C. Ces deux éléments sont placés en série avec la source \(V_{in}\) du signal. Le signal de sortie \(V_{out}\) est récupéré aux bornes du condensateur. L'amplification s'écrit :
\(A(f) = \frac{V_{out}}{V_{in}} = \frac{j 2 \pi RC f}{1+j 2 \pi RC f}\)
Le gain en décibel s'écrit ainsi :
\(G_{dB}(f) = 20 \log (|A(f)|)\)
On peut montrer que pour une certaine fréquence appelée fréquence de coupure
\(f_c = \frac{1}{2 \pi RC}\)
Le gain vaut -3dB
Lorsque \(f<<f_c\) l'amplification \(A(f)\) proche de 0 et G proche de \(-\infty\)
Lorsque \(f>>f_c\) l'amplification \(A(f)\) proche de 1 et G proche de 0.
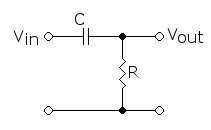
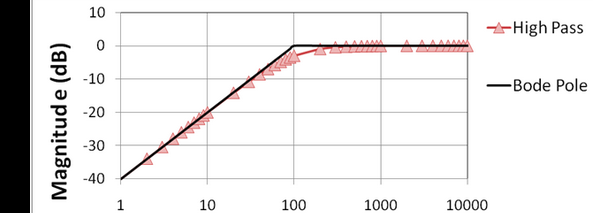
Réaliser la même étude que pour le filtre passe-bas